- 老师办公地点:综合楼815。老师电子邮件:csy@hit.edu.cn
- 助教地址:综合楼815 。助教电子邮件:kunyichenghit@126.com 、 zhutongxinhit@126.com
- 提交作业的电子邮件地址:algorithmhit2018@163.com
- 考核方式:作业+考试 80% 、 实验 20%。课后自己做。
2月27号
- 三个证明问题没有搞明白。
2月28号
- 同阶、低级、高阶、严格低级、严格高阶
- 向上取整、向下取整
3月4日
- 分治算法的设计分为两步:设计+分析。
- 分治算法的耗时主要在两个方面:子问题的个数 + 合并方式
3月11日
- 问题1
- 蚁群算法是一种用来寻找优化路径的概率型算法。
- 蚁群算法的优势在哪里?
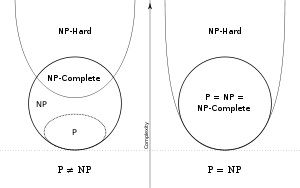
- 在数学领域,根据问题本身的复杂度是有分类的。简单来说,问题分为P问题,NP问题,NPC问题,NP-hard问题。P是多项式这个单词的首写字母,即Polynomial,[这里指多项式时间]P问题意为 总能找到相应的经典算法 在多项式时间 里面得出最优解。NP问题意为 不能确定是否能找到相应算法 能够在多项式时间内 得出最优解。NPC问题可以理解成NP问题中最难(复杂度最高)的问题,也就是说很难找到相应算法 能够在多项式时间内得出最优解。NP-hard问题可以简单理解成找不到相应算法 能够在多项式时间内得出最优解。所有对NP问题的研究都集中在一个问题上,即究竟是否有P=NP?通常所谓的“NP问题”,其实就一句话:证明或推翻P=NP。
- 简单来说就是,传统的经典算法能够解决P类问题,而NP问题,特别是NPC问题,则束手无策,于是科学家们开始想办法了,既然不能在多项式时间里得出一个最优解,那么咱们得一个较优解吧,用先验的经验知识作为启发算子,于是启发式算法诞生了,但启发式算法只能针对特定问题(比如,prime算法和kruskal算法都是经典启发式算法,在最小生成树领域比较好的效果),启发式算法不适合跨领域,但NP问题又如此之多,怎么办,于是各种仿生学理论开始引入计算机的算法领域,诞生了所谓的蚁群,粒子群,遗传,神经网络算法这些统称智能优化算法(元启发式算法)的东东来求较优解。
- 最短路径的时候,用蚁群算法和用prime算法、克鲁斯卡尔算法相比有哪些优势呢?感觉蚁群算法开销不算小,而且还容易不收敛或者陷入局部最优。说道这个问题,就得提到启发式算法和元启发式算法的巨大区别。启发式算法针对的是特定领域的特定问题,效果良好,但一旦跨领域,效果锐减。元启发式算法则具有更明显的跨领域能力,能咋相当多的领域有漂亮的效果。简单来说,prime算法、克鲁斯卡尔算法等等都是启发式算法,启发算子是:贪心策略,即是对特定问题(最小生成树)的可能有较优解法,也就是说仅适用于这一类问题。P问题只是很少的一部分,我们大部分真实场景遇到的都是NP问题,在NP问题没有彻底解决的时候,如果不想死磕—非要找到一个能在多项式时间内得出最优解的算法,我们就只能假设P!=NP,我们就能用启发式算法了,然而,启发式算法本质是某个领域特定的经验总结,一旦跨领域就失效了,所以,现在求较优解的时候,如果没有特定的好的启发式算法,我们就用智能优化算法(即元启发式算法),比如蚁群算法。这就是元启发式算法的优势,也就是蚁群算法的优势。最后说说智能优化吧,这玩意儿本质上就是掷骰子,猜,不同智能优化,就是不同的猜的规则。个人感觉蚁群算法特别吃参数,这需要慢慢调。
第一章算法性能分析
- As a rule of thumb, if the body of a loop is in O(na) then the whole loop is in O(na+1). The
exception is if you can show that the loop exits after a constant number of iterations. If a
loop runs k times regardless of n, then the loop is in O(na), even for large k.


